1. Premessa
L'acquisizione dei dati idro-meteorologici tramite reti di monitoraggio in telemisura pone la necessità di automatizzare (o semi-automatizzare) le procedure di controllo dei dati, in conseguenza della loro quantità e dell'esigenza di una tempestiva pre-validazione degli stessi, a cui seguirà una validazione vera e propria, prima dell'archiviazione definitiva.
La Regione Toscana, dispone di una rete in telemisura costituita da oltre 700 sensori per il monitoraggio meteo-climatico, dislocati, in maniera omogenea, su tutto il territorio regionale.
La pre-validazione dei dati registrati nelle stazioni in telemisura è necessaria per monitorare la registrazione dei dati in real time eliminando gli errori grossolani e/o i dati mancanti consentendo l'utilizzo immediato degli stessi senza attendere la validazione finale che di norma si conclude entro il primo semestre dell'anno successivo a quello in oggetto.
Ipotizzando un controllo mensile dei suddetti dati grezzi, la pre-validazione consentirà sia l'utilizzo dei dati dell'anno in corso per soddisfare richieste a pagamento, senza rischiare l'invio di dati affetti da errori grossolani, sia per velocizzare la validazione finale.

2. Obiettivi
L'obiettivo generale del presente lavoro è quello di avere una banca dati validata che permetta un utilizzo corretto dei dati stessi, sia per fini statistici sia per fini divulgativi. La validazione (lato sensu) del dato dovrà essere perseguita attraverso due distinte fasi di lavoro: in una prima fase il dato sarà soggetto ad una pre-validazione, ovvero una validazione sommaria del dato raggiungibile mediante l'applicazione di alcune semplici regole, che, tuttavia, consentiranno di segnalare anomalie (outliers) e/o dati mancanti; nella seconda fase, il dato verrà validato in modo definitivo ed archiviato nel DB in uso presso il Servizio Idrologico Regionale - Centro Funzionale.
Per il corretto e completo conseguimento degli obiettivi fissati nel presente lavoro, è necessario procedere ad una validazione dei dati, seguendo alcune regole stabilite per ogni tipologia di dato e segnalando le anomalie, i dati mancanti ed altri errori di varia natura, che, di volta in volta, si riscontrano nei dati stessi.

3. Metodologia di validazione dei dati pluviometrici
Attualmente il Servizio Idrologico Regionale dispone di alcuni archivi all'interno dei quali sono memorizzati in maniera organizzata tutti i dati idro-meteorologici acquisiti nelle stazioni di misura dislocate nell'intero territorio regionale. Tali dati possono essere consultati ed eventualmente scaricati sia dagli operatori sia dagli esterni attraverso diversi canali di distribuzione, quali pagine web, software dedicati, ecc.
La validazione dei dati pluviometrici riguarda principalmente i dati ad aggregazione giornaliera (formato "0-24"); tuttavia il controllo e l'applicazione delle regole stabilite sarà effettuato a partire dai dati "atomici" (dati alla minima aggregazione, registrati al quarto d'ora) riferiti al giorno in esame.
I dati al quarto d'ora validati senza nessun intervento da parte dell'operatore, garantiscono a loro volta la validazione automatica dei dati ad aggregazioni via via maggiori (oraria , giornaliera , ecc.) riferiti sempre allo stesso giorno ed alla stessa stazione.
Nel momento in cui nella fase di controllo dei dati atomici si riscontrano e si segnalano anomalie, le fasi da seguire per poter meglio interpretare la difformità del dato, sono:

• analisi dei dati temporalmente precedenti e successivi ed anche delle stazioni poste nelle immediate vicinanze della stazione in esame; se non risulta pioggia da nessuna parte e neanche negli step temporali "vicini", in tal caso è possibile assegnare valore nullo
• una presunta anomalia può essere controllata controllando le fulminazioni registrate nell'intorno della stazione in esame nello stesso intervallo di tempo in cui appare l'irregolarità del dato
• nel momento in cui si riscontra un'anomalia di qualsiasi natura relativa al dato al quarto d'ora, ove questa non possa essere corretta, tale dato deve essere considerato assente. In tal caso dovranno essere eliminati anche tutti gli altri dati al quarto d'ora riferiti allo stesso giorno (in cui si è verificata l'anomalia) e la ricostruzione del dato (cfr. paragrafo successivo) dovrà essere compiuta sul dato giornaliero.
• in ciascuna stazione si possono riscontrare alcuni dati assenti; per poter accettare il dato cumulato giornaliero (24 ore, pari a 96 step da un quarto d'ora ciascuno) devono essere presenti almeno 90 valori (~95%) di pioggia validati.

Nel dettaglio, la fase di controllo e di validazione dei dati pluviometrici, dovrà sottostare alle seguenti regole:

• Dati giornalieri (formato "0-24")
  
  1. i valori di pioggia cumulati devono essere sempre positivi
  2. i valori di pioggia cumulati devono essere inferiori ad un valore massimo, calcolato, su base storica, per ogni stazione di monitoraggio
  3. controllo dei valori di pioggia giornalieri superiori a 100 mm
  4. si richiede, per ogni stazione, un sommario confronto con le stazioni poste nelle vicinanze
  5. segnalazione dei dati mancanti

• Dati "atomici" a 15 minuti
  
  6. i valori di pioggia cumulati devono essere sempre positivi
  7. segnalazione dei dati mancanti per stazione e calcolo della loro consistenza
  8. calcolo del valore massimo per ciascuna stazione
  9. individuazione dei valori superiori ad una certa soglia prefissata
  10. individuazione di anomalie varie (es. valori dispari)
  11. calcolo della differenza (in valore assoluto) tra un valore ed il valore temporalmente precedente al fine di individuare outliers locali

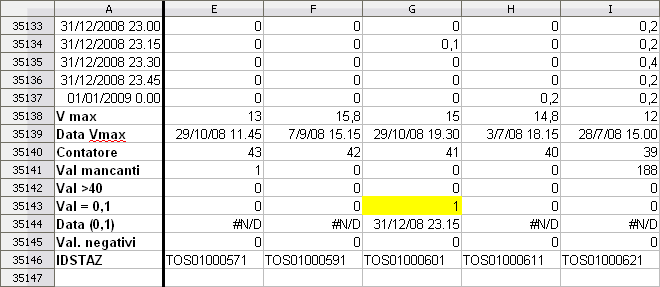Figura 1a Controlli applicati ai dati "atomici" ed individuazione degli errori

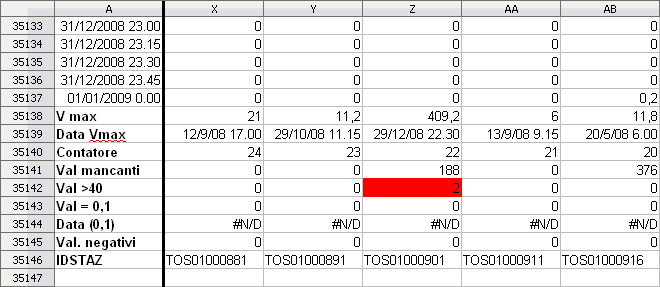Figura 1b Controlli applicati ai dati "atomici" ed individuazione degli errori

3.1 Metodi di ricostruzione dei dati giornalieri
Quando, per i motivi sopra elencati, non è possibile intervenire sul dato "atomico" al quarto d'ora, si rende necessaria la ricostruzione del dato giornaliero e l'eliminazione del dato atomico anomalo.
La ricostruzione di un dato giornaliero può essere effettuata con uno dei seguenti metodi:

• Assegnazione del valore in mm di pioggia della stazione più vicina a quella in esame
• Metodo dei topoieti (o Poligoni di Thiessen)
• Interpolazione spaziale geostatistica (es. kriging)

3.1.1 Ricostruzione mediante interpolazione geostatistica
La geostatistica, avvalendosi anche della modellazione stocastica, fornisce le basi per capire ed utilizzare le varie tecniche per la stima del valore di una variabile spaziale nelle aree ove tale variabile non è stata misurata costituendo così uno strumento per fare delle ipotesi il più possibile corrette sul continuo spaziale .
La geostatistica, dunque, fornisce un insieme di tecniche probabilistiche al fine di:

• Ricercare un modello che esprima la dipendenza spaziale dei dati
• Usare questo modello per effettuare inferenza in localizzazioni non campionate e conoscere l'errore della stima

L'ambiente si estende continuativamente in tre dimensioni ed i suoi cambiamenti sono, a volte, ovvi e ben visibili da foto aree e/o satellitari, altre volte risultano più inafferrabili (es. variazione della temperatura, della piovosità o degli inquinanti chimici). In questo ultimo caso, sono necessarie misure puntuali tramite campioni (misure di un determinato fenomeno in una precisa localizzazione spaziale) per analizzare tali cambiamenti. Al fine di creare un'informazione che sia distribuita nello spazio con caratteri di continuità è necessario utilizzare algoritmi di interpolazione spaziale che permettono di poter studiare i dati campionati sia da un punto di vista della loro disposizione nello spazio sia per quanto riguarda il loro contenuto informativo. Tra i numerosi metodi di interpolazione spaziale, l'approccio geostatistico, ed in particolare l'interpolatore di Kriging, offre una serie di vantaggi che i classici metodi di interpolazione di tipo deterministico sicuramente non hanno.
Esaminiamo nel dettaglio quali possono essere i vantaggi che si traggono da un'interpolazione eseguita con metodi geostatistici: la maggiore utilità che tale interpolazione offre è senza dubbio quello di giungere alla definizione di un modello che descriva la variabilità spaziale di un certo parametro. Inoltre, a parità di errore, richiede un numero di misurazioni minore rispetto ai metodi classici fondati sull'indipendenza della variabile. Altro aspetto da non sottovalutare è che la conoscenza della struttura della variabilità e della stima, consentono di migliorare, in termini di minori costi sia di prelievo sia, eventualmente, di analisi in laboratorio, le campagne di rilevamento dei fenomeni da studiare. Le tecniche geostatistiche si differenziano dagli altri metodi "classici" di interpolazione in quanto si fondano sul principio dell'autocorrelazione spaziale.
Infatti, una caratteristica fondamentale dell'ambiente è che le sue proprietà sono in relazione tra loro, basandosi sul principio di autocorrelazione.
L'autocorrelazione spaziale indica che luoghi vicini tra loro tendono ad avere comportamenti simili, mentre luoghi lontani tra di loro tendono ad avere comportamenti differenti, ovvero due campioni vicini tra loro hanno valori più simili di due campioni lontani (G. Ciotoli, Finoia M. G., 2005). In particolare, la geostatistica studia la variabilità spaziale dei parametri che descrivono i fenomeni ambientali oggetto di studio estraendone le regole in un quadro modellistico di riferimento e usandole per effettuare le operazioni il cui obiettivo è quello di dare soluzioni a specifiche problematiche riguardanti la caratterizzazione e la stima dei fenomeni stessi.

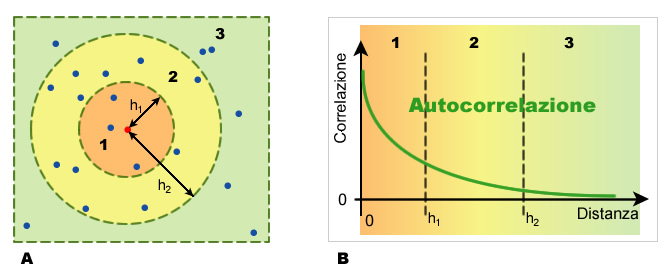Figura 2 Il principio dell'autocorrelazione spaziale

3.1.2. Il Kriging
Ogni misura zi è considerata come una realizzazione di una variabile casuale Zi; la descrizione generale di una variabile casuale si basa sulla funzione di densità di probabilità f.d.p.(Z). Tale funzione può essere discreta o continua in dipendenza della natura del fenomeno in studio; inoltre la probabilità P(Z) di individuare un valore della variabile casuale nell'intervallo (Z, Z+dZ) è espressa mediante l'equazione:

P(Z) = f(Z)dZ

Tra i molteplici metodi di distribuzione dei dati, vale la pena ricordare la distribuzione Gaussiana (o Normale), espressa dalla seguente formulazione matematica:

f(Z) = 1/(2P)s exp (-(Z-Zm)2 / 2 s2)

con:
Zm = valore medio
s = deviazione standard (s2 = varianza)

Dopo questa breve premessa circa la natura dei dati osservati, cerchiamo di capire come tali misure vengono utilizzate al fine di effettuare delle stime in luoghi ove la variabile non è stata direttamente osservata. Per poter ricostruire la superficie cercata è necessario interpolare i dati disponibili per stimare i valori dove non si hanno campioni. In questo senso il kriging ci viene incontro, in quanto da una soluzione al problema della stima basato su un modello continuo di variazione spaziale stocastica. Esso fa il miglior uso della conoscenza della variabile, prendendo in considerazione il modo in cui una proprietà varia nello spazio attraverso il modello del variogramma che è stato scelto e validato nelle fasi precedenti dell'analisi variografica. Pertanto, è possibile asserire che il kriging costituisce la fase più propriamente predittiva dell'analisi geostatistica.
Esistono diversi tipi di kriging, tra cui kriging ordinario (ordinary kriging) e kriging universale (universal kriging), per diverse tipologie di variabili. Ciò che li differenzia è il tipo di variabile usata: il kriging ordinario può lavorare solo con variabili stazionarie del secondo ordine (presentano cioè media costante e varianza dipendente solo dal lag muovendosi da punto a punto), il kriging universale può invece lavorare anche con variabili non stazionarie (che presentano cioè un drift). Come anticipato una delle assunzioni fatte nel kriging ordinario è la stazionarietà del dato da stimare. Questo significa che muovendosi da una zona ad un'altra del campo S la media dei valori è pressochè costante. Quando invece esiste un significativo trend spaziale del dato (caratteristica intrinseca del dato stesso che fa si che la media dei valori non sia costante ma vari da punto a punto) questa assunzione viene meno. La condizione di stazionarietà del dato può essere comunque ristabilita attraverso l'introduzione di una funzione deterministica che descriva il drift, cioè l'andamento della media, in modo da poter isolare il residuo, cioè la parte aleatoria del dato. Il kriging universale quindi modella e sottrae il drift presente nel dato tramite una funzione deterministica, ed analizza la sola componente aleatoria (residuo).
Nel kriging, sia ordinario che universale, tramite un sistema di equazioni lineari, si assegnano i pesi per i campioni circostanti al punto analizzato che minimizzano la varianza totale degli errori. Solitamente i quattro cinque campioni più vicini contribuiscono per l'80% del peso totale, il restante 20% viene assegnato all'incirca ad altri dieci punti vicini. Si hanno vari fattori che influenzano i pesi tra cui:

• i campioni vicini portano più peso di quelli lontani e l'entità del peso dipende dalla loro posizione e dal variogramma;
• i campioni raggruppati in un certo intorno portano meno peso di quelli isolati.

Il metodo del Kriging è notoriamente conosciuto come un interpolatore BLUE (Best Linear Unbised Estimator); infatti la stima migliore (best) si ottiene minimizzando la varianza della stima, ovvero imponendo uguale a zero il valore della derivata della varianza stessa rispetto ai ponderatori ?; lineare (linear) significa che la stima viene effettuata utilizzando modelli lineari. Una stima corretta (unbiased) si ottiene intimando zero il valore della media della stima, evitando così di introdurre errori sistematici.
Nel dettaglio, vediamo come avviene il calcolo dei suddetti pesi; appare, inoltre, opportuno ricordare che il kriging è una tecnica geostatistica d'interpolazione per mezzo della quale si perviene ad una stima z*(x0) della variabile tramite una media pesata dei valori sperimentali assunti dalla stessa variabile nei punti campionati. L'assunzione fondamentale del kriging è che i dati siano una realizzazione di un processo spazialmente autocorrelato più un errore random indipendente:

Z(x) = m(x) + Y(x)

dove Z(x) è la variabile regionalizzata (variabile che assume diversi valori in base alla posizione spaziale nel campo di studio), m(x) rappresenta la componente strutturale (il trend), mentre Y(x) è la manifestazione delle irregolarità locali presentate dal fenomeno (componente aleatoria).
Ad esempio, in una zona all'interno di un'area inquinata, i valori di un certo agente inquinante sembrano variare casualmente (componente aleatoria o casuale), mentre ci sono zone all'interno della stessa area che mostrano valori più elevati che in altre (aspetto strutturato del fenomeno).
In genere, possiamo avere casi estremi in cui la componente casuale sia assente e la VR potrebbe essere descritta dal solo trend rappresentabile attraverso una funzione matematica. Viceversa, esistono alcuni casi in cui il trend è completamente assente oppure costante nel dominio spaziale esaminato. Tuttavia, anche in presenza di trend, è opportuno analizzare l'informazione contenuta nella componente residua (casuale): infatti, le fluttuazioni descritte da questa componente non sono errori, ma delle caratteristiche tipiche dei dati osservati. In questo caso la correlazione spaziale viene studiata tenendo conto di questa componente residua. Pertanto, obiettivo della geostatistica è ricercare le due componenti suddette a partire da osservazioni frammentarie (i campioni misurati), in modo da poter utilizzare il modello per effettuare delle stime in localizzazioni non campionate.
Come detto in precedenza, ogni variabile regionalizzata è descritta da una distribuzione probabilistica; con i modelli Gaussiani, per poter descrivere completamente la variabile sono sufficienti due parametri: la media e la varianza.
Una stima z*(x0) della variabile da interpolare nel punto x0 si ottiene mediante una combinazione lineare di valori noti z(xi) nei punti xi:

z*(x0) = Si ?i z(xi)

Le stime z* sono delle realizzazioni della funzione aleatoria Z*(x) (cfr. paragrafo 1), che quindi si può esprimere come:

Z*(x0) = Si ?i z(xi)

A questo punto è necessario determinare i coefficienti ?i evitando, come detto in precedenza, che l'errore

E(x0) = Z(x0) x Z*(X0)

sia sistematico (ovvero costante al ripetersi della misurazione) e cercando di ottimizzare la stima. Per ottenere tali risultanze è essenziale imporre i seguenti vincoli:

• Media (E(x0)) = 0
• Varianza (E(x0)) minima

4. Metodologia di validazione dei dati idrometrici
La validazione dei dati idrometrici consiste in un'accurata analisi del dato di livello "atomico", ovvero a 15 minuti, che viene eseguita su tutti gli strumenti automatici installati sul territorio regionale. Tale operazione è di fondamentale importanza per dare la possibilità agli utenti di usufruire di una fonte di dati consistente per analisi dirette e/o eventuali elaborazioni nei diversi campi di applicazione (confronti con i dati storici, derivazioni di portate, etc..).
Di norma viene effettuata in due distinte fasi, denominate, rispettivamente, prevalidazione e validazione.
Tutto il processo di validazione dei dati idrometrici si basa sul concetto della continuità del dato, inteso come espressione del livello idrometrico di una nota sezione monitorata. La conoscenza degli strumenti di rilevazione, del corso d'acqua, della sezione, nonchè l'esperienza degli operatori, è fondamentale per raggiungere l'obiettivo di una elevata qualità del dato finale.

4.1. Il processo di prevalidazione dei dati
L'obiettivo della prevalidazione è quella di confermare, ricostruire, segnalare e/o cancellare i valori di altezza idrometrica registrati dagli strumenti in telemisura.
Il foglio elettronico di calcolo è predisposto per fornire all'operatore i principali dati della serie numerica a 15 minuti di una stazione idrometrica. Tali dati consistono nel valore massimo e nel valore minino, il numero di dati mancanti della serie numerica e la lista dei numeri derivanti dalle differenze di dati conseguenti, il cui valore è maggiore del differenziale massimo impostato per quella sezione (delta). I dati statistici (precedentemente descritti) e la visualizzazione degli stessi su grafico sono lo strumento principale per l'interpretazione della serie numerica da parte dell'operatore, al fine rilevare e correggere gli errori strumentali.
In generale, nelle operazioni di prevalidazione la ricostruzione dei dati verrà effettuata in presenza di:

• dati mancanti fino a 1 ora (4 dati);
• dati palesemente errati (outliers) fino ad 1 ora (4 dati).

La ricostruzione dei dati avviene tramite interpolazione lineare.
La cancellazione dei dati viene effettuata quando la serie di valori palesemente errati è uguale o superiore a 12 ore continuative (48 dati).
Le situazioni intermedie tra quelle sopra descritte, ovvero ricostruzione (per i dati fino ad 1 ora) e cancellazione (dati mancanti o palesemente errati per 12 ore continuative) richiedono un'analisi approfondita, che viene valutata nella succesiva fase di validazione.

4.2. Metodi di ricostruzione e validazione dei dati
L'obiettivo della validazione è quella di confermare, correggere, ricostruire, segnalare e/o cancellare i valori di altezza idrometrica media (o parte di essa) registrati dagli strumenti in telemisura, già precedentemente prevalidati.
Le operazioni di validazione dei dati vengono eseguite, come per la prevalidazione, con il foglio elettronico di calcolo in modalità semiautomatica.
La prima operazione effettuata è la verifica sui dati mancanti o evidentemente errati superiori a 1 ora e fino a 12 ore (eventualmente presenti e segnalati durante la prevalidazione); la verifica consiste nel controllare le sezioni a monte e a valle (se presenti) nel medesimo periodo e valutare se sussistono le condizioni per ricostruire i dati (tramite similitudine, aggiungendo/sottraendo un numero k ai dati della serie completa, ipotizzando la conservazione della forma). In caso positivo, l'operazione viene "marcata" affiancando al dato ricostruito la lettera "R", oppure, non essendoci le condizioni, i dati vengono considerati mancanti.
Di seguito un esempio di ricostruzione dei dati idrometrici su un corso d'acqua principale: il livello idrometrico da ricostruire viene riportato su grafico (linea blu di Fig. 3), con una finestra temporale variabile a seconda del numero di dati mancanti, con il livello idrometrico di una stazione di misura posta sullo stesso corso d'acqua, a monte o a valle (linea rossa di Fig. 3).

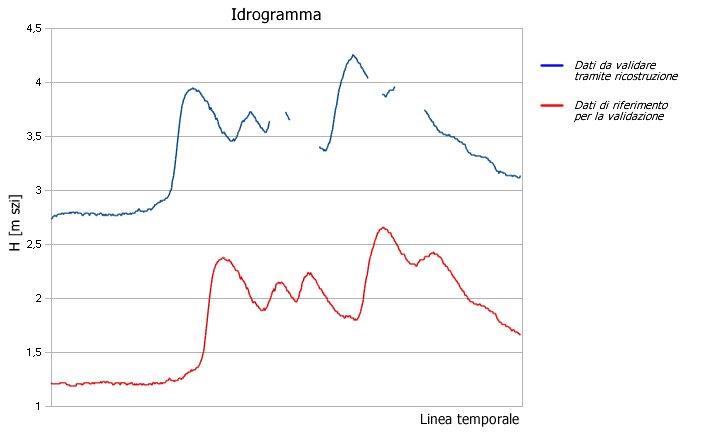Figura 3 Esempio di idrogramma da ricostruire

Dapprima graficamente, poi numericamente, vengono individuate le parti di dati della serie completa interessate dalla ricostruzione (dati di base); l'operazione finale consiste nel traslare i dati di base sommando o sottraendo il differenziale medio (numero k) tra le due altezze idrometriche (linea gialla di Fig. 4).

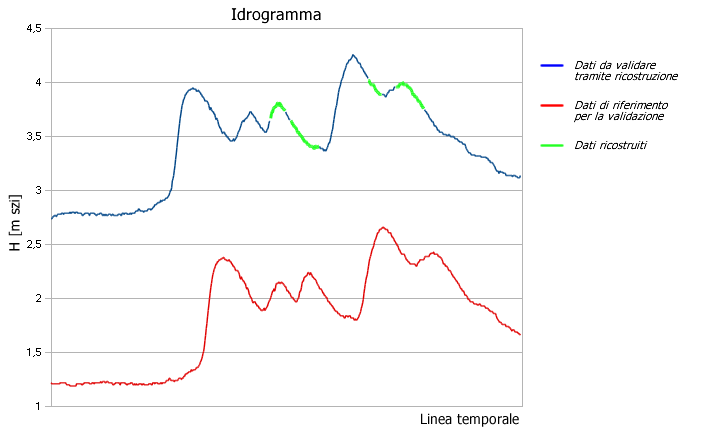Figura 4 Esempio di idrogramma ricostruito

La possibilità di effettuare questo tipo di operazione dipende da molteplici fattori, tra cui la presenza e il tipo di apporto di uno o più corsi d'acqua tra le due sezioni, la distanza tra le sezioni, la loro forma, l'andamento dell'idrogramma, etc... Nei casi ambigui o che necessitino di informazioni non disponibili, i dati assenti non verranno ricostruiti e saranno considerati ufficialmente mancanti.
Successivamente la serie di dati viene confrontata con le verifiche di congruenza effettuate nel periodo oggetto di validazione e/o con le tarature effettuate dalla ditta di manutenzione dello strumento in telemisura nel medesimo periodo.
Il confronto dei dati registrati con quelli realmente riscontrati durante le verifiche e le tarature permetterà di confermare, correggere o cancellare la serie di dati idrometrici in elaborazione.
La conferma o la correzione dei dati avviene, per ogni singola stazione idrometrica, considerando l'eventuale scarto tra la lettura diretta e il valore registrato dallo strumento. In generale, non viene effettuata nessuna modifica/taratura fin quando lo scarto è pari a 2 cm. Considerando la complessità degli strumenti, la variabilità dei sensori delle ditte fornitrici, le differenti caratteristiche di ogni sito, ma anche il periodo dell'anno in cui è stato controllato lo strumento, etc.., il valore di 2 cm è puramente indicativo; è proprio in questa fase, infatti, che l'operatore risulta indispensabile nella valutazione dei parametri sopra descritti e delle decisioni conseguenti. La cancellazione dei dati avviene nei casi in cui non sia possibile riuscire a determinare l'esatta entità dell'errore strumentale.
Nel caso di differenze accertate superiori a 2 cm, vengono effettuate delle interpolazioni lineari tra gli scarti relativi a due verifiche consecutive. Tutti i dati puntuali (15') di questa interpolazione lineare vengono successivamente sommati al valore registrato dalla telemisura, determinando il valore idrometrico validato.
Nella Figura 5 è rappresentata una serie di dati idrometrici prevalidati (linea rossa) con la stessa serie di dati validata. Dopo la verifica dell'asta idrometrica e la taratura strumentale le due linee coincidono essendo lo scarto pari a zero.

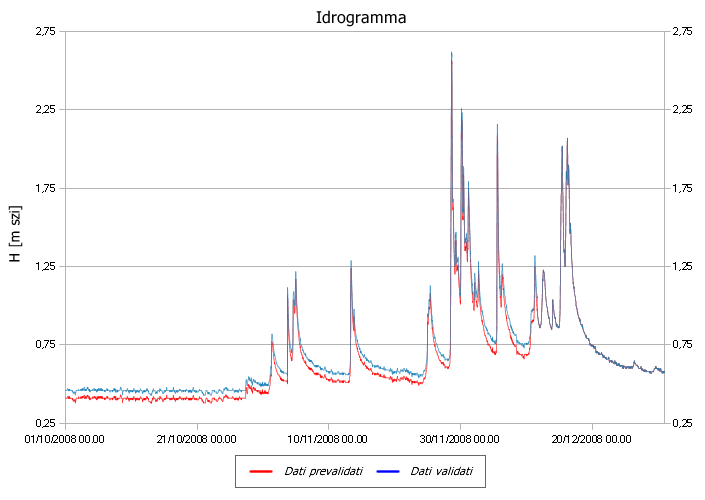Figura 5 Esempio di idrogramma di validazione

5. Metodologia di validazione dei dati freatimetrici
L'acqua di un corpo idrico sotterraneo (falda) è generalmente sottoposta a pressione. Ad ogni falda viene associata una superficie piezometrica, che rappresenta la quota che raggiungerebbe l'acqua se fosse libera di defluire verso l'esterno.
Le stazioni freatimetriche automatiche del Servizio Idrologico, attivate in corrispondenza di pozzi e tubi piezometrici, rilevano la profondità di tale superficie dal piano di campagna, oltre alla temperatura e conducibilità dell'acqua di falda.

Oltre alla sonda termofreatimetrica, le stazioni di monitoraggio installate, sono costituite da un datalogger per l'acquisizione e memorizzazione dei dati acquisiti e dal sistema di trasmissione dati (GSM-GPRS).
La sonda è composta da cella di pressione ceramico/capacitiva, per la determinazione del livello di falda, da un sensore di temperatura acqua ed un sensore per la misura della conducibilità dell'acqua; la stazione è dotata inoltre di un tubetto di compensazione per riequilibrare la misura freatimetrica con le variazioni della pressione atmosferica.

L'intervallo di acquisizione dello strumento è orario; i dati atomici, una volta validati, vengono aggregati e mediati per ottenere e fornire un valore di "soggiacenza media giornaliera".

5.1 Il processo di pre-validazione dei dati
I dati atomici così come registrati subiscono un processo di pre-validazione automatica, che ha lo scopo di eliminare eventuali outliers presenti, mediante l'applicazione di alcune semplici regole, in primis la definizione di un range di oscillazione "orario" massimo ammissibile del livello piezometrico (differenza tra il valore di un dato atomico e quello precedente).
In condizioni naturali infatti, ad esclusione delle falde freatiche superficiali o di subalveo, la superficie di una falda sotterranea è caratterizzata da un graduale e lento movimento di risalita e discesa nel tempo, quindi dall'assenza di brusche e repentine oscillazioni.
L'analisi delle serie storiche, oltre a consentire l'identificazione di un trend orario di crescita e descrescita della superficie di falda, permette di definire, per ogni punto di controllo, i livelli piezometrici estremi annuali, che determinano l'intervallo di oscillazione naturale della falda (Lmax e Lmin). Tali parametri vengono verificati e aggiornati annualmente.

5.2 Il processo di validazione dei dati
Il processo successivo consiste nella validazione del dato atomico, operazione che tiene esclusivamente conto degli interventi di manutenzione programmata effettuati nell'arco dell'anno sulle stazioni, in particolare quando viene effettuata la ritaratura dello strumento (dovuta alla deriva strumentale), quindi il riallineamento tra il valore automatico acquisito da quest'ultimo e quello effettivamente verificato in situ dall'operatore.
Tale errore strumentale viene quindi distribuito sui valori atomici acquisiti tra il giorno del riallineamento ed il precedente intervento di manutenzione, per il quale si dispone del valore effettivo della profondità della falda (acquisito con freatimetro manuale).
Tale operazione comporta quindi una correzione del dato atomico.

Nel processo di validazione dei dati atomici non viene effettuata alcuna ricostruzione dei dati mancanti.

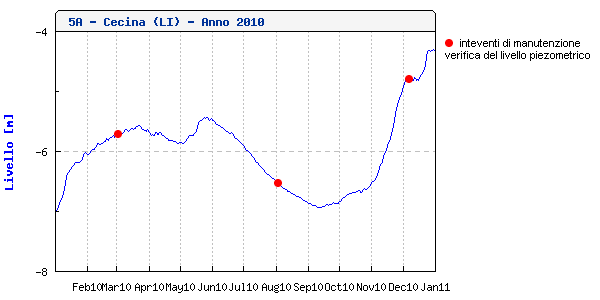Figura 6 Esempio di serie validata per l'anno 2010, stazione 5A [TOS19000601] - Cecina

Per Soggiacenza media giornaliera si intende la media aritmetica dei valori atomici rilevati in 1 giorno (24h), dalle ore 00:00 alle ore 24:00.
Sulla base dell'esperienza maturata nell'ambito del monitoraggio quantitativo automatico dei Corpi Idrici Regionali (CIS), è stato individuato quale numero minimo di dati atomici sufficienti per il calcolo del suddetto valore medio giornaliero, il valore di sei registrazioni orarie (di 24); là dove si disponga di un numero di dati atomici inferiore, il dato giornaliero è considerato mancante.

6. Metodologia di validazione dei dati termometrici
Le serie termometriche talvolta possono presentare valori mancanti o intervalli temporali di valori mancanti, soprattutto quando, in una medesima località, si sono succeduti nel tempo vari osservatori. In altre circostanze le lacune nei dati possono essere altresì dovute a problemi di trasmissione e ricezione del dato. La serie di dati può inoltre presentare per brevi periodi deviazioni significative rispetto ai valori rilevati nei giorni precedenti e/o seguenti, dovute ad improvvisi guasti del sensore di rilevamento.
La stima e la ricostruzione di tali valori richiede però una scelta operativa oculata e basata soprattutto sulla correlazione con stazioni limitrofe o vicine funzionanti durante il periodo temporale privo o carente di dati campionari. L'applicazione però di apposite tecniche che consentano di ricavare dalle stazioni limitrofe i dati mancanti, deve essere preceduta, non solo dalla verifica che le stazioni presentino analoghi o compatibili caratteri morfologici territoriali, cioè stazioni appartenenti alla stessa categoria di rilevazione di dati (di pianura, di versante, di crinale, di valle o fondovalle, urbane, ecc...), ma anche dall'accertamento che presentino compatibilità tra i loro dati campionari, ovverosia è necessario provare la mancanza o quasi di differenze tra i dati registrati e l'analogo andamento nel tempo.

6.1 Il processo di pre-validazione dei dati
Quotidianamente viene eseguito dall'operatore validatore un controllo di qualità sul dato registrato alla minima aggregazione (15') negli ultimi 2 giorni (fase di pre-validazione).
Questo al fine di individuare le anomalie più grossolane e gli eventuali malfunzionamenti dei sensori installati sulle stazioni meteorologiche dislocate nel territorio regionale.
Per l'individuazione dei valori alterati, è stato inoltre costruito con la sezione informatica anche un "Report Giornaliero" che evidenzia quelle stazioni che non registrano il dato da almeno 2 giorni, che possono essere pertanto sfuggite all'individuazione diretta da parte del validatore.
Una volta riscontrata effettivamente un'anomalia sul dato, l'utilizzo di un software consente di inserire e modificare un dato originale, pur mantenendo la storia delle modifiche occorse.
Al fine di individuare errori sistematici di misura sono state sviluppate e sono tutt'ora in corso di ulteriore aggiornamento, metodologie di pre-validazione basate su processi matematici, fisici e informatici automatizzate, in grado di fornire un ulteriore apporto all'operatore validatore.
La ricostruzione del dato inesatto o la ricostruzione di quello mancante è effettuata su un periodo generalmente breve, per minimizzare il più possibile l'errore che commettiamo in fase di pre-validazione.
Nella prima fase di validazione (pre-validazione) la ricostruzione del dato termico è eseguita con l'utilizzo di tecniche di interpolazione lineare, senza ricorrere necessariamente all'utilizzo, come termine di confronto, della/e stazione/i vicina/e.
Se la stazione insiste con misure di dati anomali viene disattivata dal tempo reale e segnalata alla ditta responsabile della manutenzione, che provvederà alla eventuale sostituzione/riparazione del sensore entro i termini contrattuali predefiniti.

6.2 Metodologia di validazione dei dati
Mentre il processo di pre-validazione è ripetuto giorno dopo giorno, la validazione definitiva viene effettuata allo stato attuale generalmente durante l'anno successivo a quello in corso.
Anche in tal caso la stima dei dati mancanti o ritenuti errati in una stazione è eseguita principalmente per mezzo di procedure statistiche considerando sempre i dati registrati alla minima aggregazione.
In tal caso però, dovendo generalmente ricostruire periodi di dati mancanti più lunghi, è necessario in primo luogo definire le correlazioni esistenti tra le singole stazioni meteorologiche di rilevamento, anche con i criteri già sopra citati.
Come ulteriore riprova, la validazione viene eseguita anche sul dato giornaliero, che è il dato ultimo in prevalenza utilizzato dagli utenti.
In particolare, per periodi prolungati di dati assenti, è stato possibile ricostruire i valori mancanti con indagini fondate principalmente su regressioni statistiche, individuando le stazioni limitrofe più correlate alla stazione di riferimento, e definendo tra queste quella con il maggior grado di correlazione alla stazione in oggetto. La complessa costruzione di fogli elettronici opportunamente elaborati sia per la validazione dei dati registrati alla minima aggregazione, sia per quelli giornalieri, ha consentito lo svolgimento di una efficace procedura di validazione.

7 Procedura per la stima del Coefficiente di Deflusso
Il coefficiente di deflusso (Annali idrologici, parte seconda, sezione C) di un bacino idrografico di un determinato intervallo di tempo è definito come il rapporto tra l'altezza di deflusso e l'altezza di afflusso meteorico relative all'intervallo. Per altezza di deflusso di un bacino idrografico in un determinato intervallo di tempo si intende lo spessore dello strato d'acqua (misurato in mm) ottenuto dal rapporto del volume d'acqua defluito durante quell'intervallo di tempo (portata Q) e la superficie del bacino imbrifero (in modo da ottenere un valore in mm della lama d'acqua uniformemente distribuito sulla superficie del bacino facilmente confrontabile con le precipitazioni cadute).
Per afflussi (mm) in un determinato bacino idrografico si intendono le piogge lorde cadute a terra considerando le precipitazioni che interessano il bacino idrografico sotteso dalla sezione di chiusura considerata (idrometro di riferimento). In linea teorica il coefficiente di deflusso (in seguito CD) è compreso tra 0 e 1. Tuttavia si possono riscontrare CD con valori superiori a 1. I motivi possono essere ricondotti ai seguenti:

1. precipitazioni nevose: non registrate dai pluviometri (se non di tipo riscaldato) ma che entrano nel computo degli afflussi una volta sciolte;
2. tempi di corrivazione: il tempo che intercorre tra la caduta della goccia di pioggia e il raggiungimento della sezione di riferimento. In alcuni casi, precipitazioni alla fine del mese producono il deflusso all'inizio del mese successivo.
3. letture strumentali e scale di deflusso: gli strumenti possono essere soggetti a errori così come la definizione di scale di deflusso potrebbe portare a errori nella determinazione della portata a fronte di un'altezza idrometrica misurata;
4. caratteristiche del bacino, ivi comprese le opere di regimazione delle portate (es.: dighe).

Per i motivi suddetti, come anticipato, può capitare che la valutazione mensile dei CD porti a valori superiori a 1. Tuttavia, il calcolo del CD annuo, inteso come rapporto tra la somma annuale dei deflussi sulla somma annuale degli afflussi, dovrebbe sempre dar luogo a un CD compreso tra 0 e 1. Il caso in cui il CD sia superiore a 1 può essere ricondotto soltanto alle cause 3) e 4) dettagliate in precedenza, visto che le prime due vengono, di norma, riassorbite nel bilancio annuale.
Da notare che anche negli annali pubblicati dal SIMN fino all'anno 1995 sono presenti, per alcuni mesi, negli idrometri toscani CD superiori a 1.

7.1 Metodologia

1. Afflussi
   Gli afflussi vengono determinati e validati per ogni bacino sotteso dagli idrometri utilizzando una metodologia geostatistica, descritta in maniera più particolareggiata clicca qui
2. Deflussi
   La portata di un corso d'acqua è definita come il volume che defluisce nell'unità di tempo attraverso una sezione data. La misura di tale grandezza fisica si affronta per via indiretta andando a misurare una o più grandezze fisiche ad essa legate.
   Le portate ai diversi idrometri sono state ottenute utilizzando le scale di deflusso definite per ciascuno di essi. La scala di deflusso è una legge empirica che correla le altezze idrometriche (lette dalle aste idrometriche o, come avviene ormai negli ultimi anni, attraverso le registrazioni dei sensori idrometrici) alle portate. Tale legge viene verificata utilizzando delle vere e proprie misure di portata liquida associate alla altezza idrometrica rilevata in quell'istante.
   Una delle caratteristiche più importanti delle scale di deflusso è la sua variabilità nel tempo. Il problema risulta complesso, in quanto possono intervenire una serie di fattori, di origine sia naturale (piene sia ordinarie che straordinarie) che antropica (lavori in alveo, ponti,...), ad indurre modificazioni alla morfologia dell'asta fluviale, e quindi al regime idrometrico che in essa si instaura in occasione di eventi naturali estremi. È importante sottolineare che la determinazione del valore di portata mediante la scala di deflusso risulta tanto più affidabile quanto più tale valore rientra nel campo delle misure sperimentali effettuate. Molto spesso, invece, la stima delle portate di piena avviene necessariamente estrapolando la scala di deflusso oltre il campo delle misure dirette (utilizzando modelli idraulici o eseguendo una semplice estrapolazione del ramo delle portate misurate): in tal caso gli errori di stima possono essere anche molto elevati e, in particolare, sono crescenti all'aumentare dell'altezza idrometrica (ramo della scala di deflusso "estrapolato").
   I dati idrometrici sono stati validati utilizzando la metodologia esposta in dettaglio clicca qui

7.2 Avvertenza
I coefficienti di deflusso pubblicati sono ottenuti sulla base della metodologia sopra esposta. Metodi diversi del calcolo degli afflussi (piogge) sul bacino sotteso dall'idrometro, così come l'utilizzo di scale di deflusso diverse (che si ripercuotono sui deflussi, portate) possono produrre risultati diversi. Il SIR declina ogni responsabilità derivante dall'utilizzo dei dati pubblicati.

8 Bibliografia

• Gian Camillo Cortemiglia – Università degli Studi di Genova – Dipartimento per lo Studio del Territorio e delle sue Risorse (DIP.TE.RIS.), Facoltà di Scienze Matematiche Fisiche e Naturali - Quaderno N.3 - Messa a punto di una procedura per l’analisi climatica delle serie termo pluviometriche storiche italiane con relativa applicazione esemplificativa alla serie storica di Genova (1833-2001)
• Mariani Luigi – Università degli Studi di Milano, Dipartimento di Produzione Vegetale - Rivista Italiana di Agrometeorologia 48 – 56(2) 2006 - Alcuni metodi per l’analisi delle serie storiche in agrometeorologia
• Tridello G., Chiaudani A., Rech F., Tardivo G., Meneghini P., Cecchetto F., Delillo I., Orlandini S., Di Stefano V., Bartolini G., Mariani M., Cola G., Borin M., Berti A., Bonamano A. – Indagine regionale nel Veneto, per il monitoraggio dei cambiamenti climatici e del loro impatto in agricoltura